¿QuĆ© posibilidades hay de ganar algo (incluido un reembolso) cuando juegas un dĆ©cimo de la loterĆa de Navidad? Se suele decir que esta probabilidad es del 15%: los chatbots consultivos explican que esta cifra resulta de dividir el nĆŗmero de premios, 15.304, por los cien mil nĆŗmeros posibles (de 00000 a 99999).
Lo primero que nos viene a la mente en estas ocasiones son pelĆculas del Viejo Oeste con escenas de vaqueros, indios y caballos. A veces hay caballos sin jinete y otras veces hay caballos con dos jinetes. Pues bien, con los nĆŗmeros de loterĆa ocurre lo mismo: si suponemos que los caballos son los nĆŗmeros y los premios son los jinetes, veremos que un mismo nĆŗmero puede llevar mĆ”s de un premio.
Por ejemplo, en el sorteo especial de Navidad de 2024, el nĆŗmero 71340 recibiĆ³ una piedra (aparecĆa en una de las cuerdas de la Tabla 8) y tambiĆ©n fue premiado por acertar los dos nĆŗmeros al final del tercer premio -11840-. AdemĆ”s, obtuvo un reembolso porque coincidiĆ³ con la rescisiĆ³n de Fat Man - 72480 -. Si estuviĆ©ramos hablando del nĆŗmero 72.440, tambiĆ©n habrĆa ganado el premio por acertar cientos de botes (nĆŗmeros 72.400 al 72.499, excluyendo el primer premio).
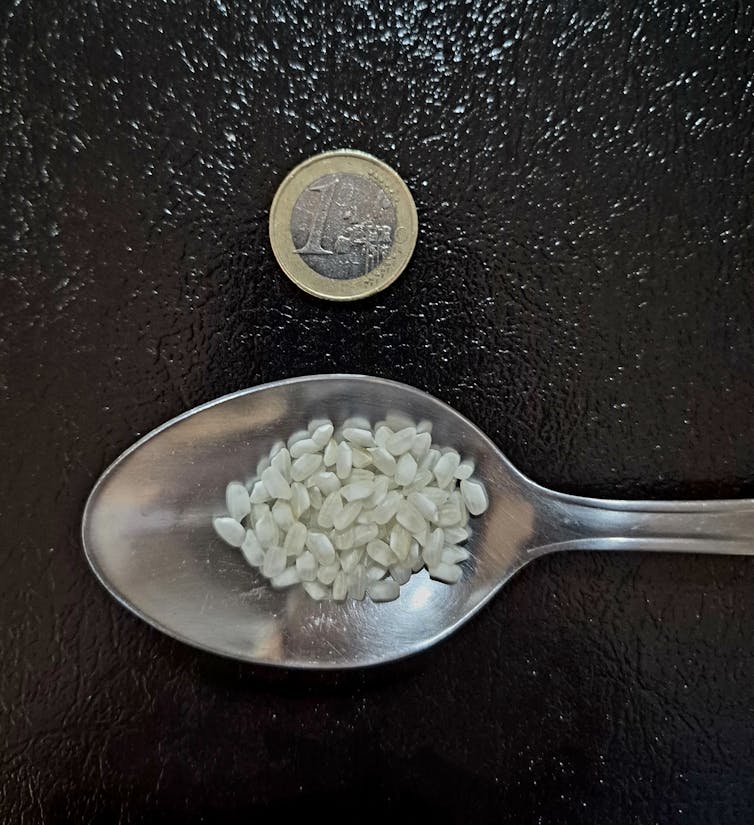
Una cuchara sopera que contiene 100 granos de arroz. Paco Pedroche. Caballos y jinetes
Como hay nĆŗmeros con mĆ”s de un premio, el nĆŗmero de nĆŗmeros con probabilidades de ganar un premio (es decir, el caballo que llevarĆ” a los jinetes) es menor que el nĆŗmero de premios (nĆŗmero de jinetes). Por tanto, para calcular la probabilidad de ganar algo en el sorteo de Navidad no podemos simplemente dividir el nĆŗmero de premios entre 100.000 nĆŗmeros.
Un cĆ”lculo mĆ”s aproximado de la probabilidad de ganar algo al jugar diez consiste en eliminar de los posibles premios aquellos nĆŗmeros que seguro que ganarĆ”n al menos dos premios. Es decir, hay caballos con dos jinetes que se pueden reconocer fĆ”cilmente incluso antes de que comience el sorteo. Estos nĆŗmeros son los que aparecen en el programa de premios titulado: "999 premios de 1.000€ cada uno para billetes cuyas dos Ćŗltimas cifras sean iguales y se repartan equitativamente entre los de quien gane el premio primero".
La probabilidad es inferior al 15%.
En el sorteo de Navidad de 2024, los 999 nĆŗmeros premiados con este premio fueron los nĆŗmeros XXXX80: 00080, 00180, hasta el 99.980. Este conjunto excluye el premio mayor en sĆ, 72.480. Estos nĆŗmeros 999 tambiĆ©n recibieron un reembolso por hacer coincidir el Ćŗltimo dĆgito (0, en este ejemplo). Todos esos caballos (nĆŗmeros) llevan al menos dos jinetes (premios).
Por tanto, podemos afirmar que los nĆŗmeros a los que se les ha concedido algo (incluido el reembolso) serĆ”n como mĆ”ximo 15.304 menos 999, es decir 14.305. De esta forma, una medida mĆ”s aproximada de la probabilidad de ganar algo en el sorteo del premio mayor es como mĆ”ximo del 14,3% (como ya afirmĆ³ el profesor JosĆ© Manuel LĆ³pez, redondeando al 14%).
Un grano de arroz en treinta platos de paella
Las IA consultivas son precisas a la hora de predecir la probabilidad de ganar el premio mayor, ya que es un nĆŗmero entre 100.000 nĆŗmeros posibles, lo que significa que la probabilidad es 0,00001 o, expresada como porcentaje, 0,001%. AdemĆ”s, la IA puede proporcionar una buena analogĆa para visualizar este nĆŗmero. Entre los comĆŗnmente utilizados en la literatura prefiero el propuesto hace muchos aƱos por el matemĆ”tico y divulgador JosĆ© Luis MuƱoz, que utilizaba granos de arroz. Por supuesto, como valenciano, trasladarĆ© esa analogĆa a los platos de paella.
Para tener una idea de lo pequeƱos que son los granos tĆpicos del arroz para paella, cuenta 100 granos y ponlos en una cucharada. VerĆ”s que queda mucho espacio libre. Estimemos cuĆ”nto pesan cien mil granos de arroz. En los artĆculos cientĆficos sobre agronomĆa del arroz, se suele utilizar como medida de peso una unidad llamada PMG (peso de mil granos).
Para nuestro propĆ³sito consideraremos un tipo de arroz ligero con un PMG de 25 g, es decir, mil granos de arroz que pesan 25 gramos. Por tanto, cien mil granos pesan 2,5 kg. SegĆŗn fuentes cercanas (mi pareja), una raciĆ³n tĆpica de paella valenciana ronda los 80g por persona. Es decir, con 100.000 granos de arroz (2,5 kg) tenemos unas 31,25 porciones de paella, que aproximadamente podemos estimar en 30 para tener un nĆŗmero redondo. AsĆ que podemos decir que ganar el premio mayor de Navidad es como adivinar dĆ³nde se esconde un determinado grano de arroz entre 30 platos de paella.
.webp)
0 Comentarios